Allan deviation analysis

Allan deviation analysis is a technique for quantifying the different sources of error affecting IMU measurements. The imutools.IMUBase class features methods to fit a model to averaging times \(\tau\) and Allan deviation estimates \(\sigma\).

# Set up
import warnings
import importlib.resources as rsrc
import os.path as osp
import numpy as np
import xarray as xr
import matplotlib.pyplot as plt
import skdiveMove.imutools as imutools
from scipy.optimize import OptimizeWarning

For demonstrating the methods available in the imutools.IMUBase class, IMU measurements from an Android mobile phone were collected for 6 hours at 100 Hz frequency, but subsequently decimated to 10 Hz with a forward/backward filter to avoid phase shift. The phone was kept immobile on a table, facing up, for the data collection period. Note that two sets of measurements for the magnetometer and gyroscope were recorded: output and measured. The type of measurement and the sensor axis constitute a multi-index, which provide significant advantages for indexing, so these are rebuilt:

icdf = (rsrc.files("skdiveMove") / "tests" /
        "data" / "samsung_galaxy_s5.nc")
s5ds = (xr.load_dataset(icdf)  # rebuild MultiIndex
        .set_index(gyroscope=["gyroscope_type", "gyroscope_axis"],
                   magnetometer=["magnetometer_type",
                                 "magnetometer_axis"]))
imu = imutools.IMUBase(s5ds.sel(gyroscope="measured",  # use multi-index
                                magnetometer="measured"),
                       imu_filename=icdf)

Note that the data collected are uncorrected for bias. It is unclear whether Android’s raw (measured) sensor data have any other corrections or calibrations, but the assumption here is that none were performed.

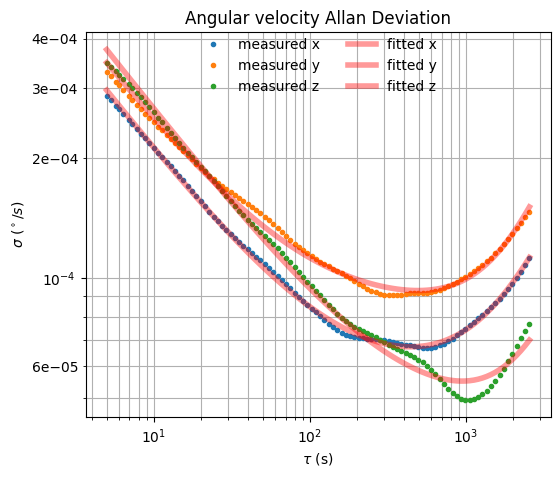
The first step of the analysis involves the calculation of \(\tau\) and \(\sigma\). The choice of \(\tau\) sequence is crucial.

maxn = np.floor(np.log2(imu.angular_velocity.shape[0] / 250))
taus = ((50.0 / imu.angular_velocity.attrs["sampling_rate"]) *
        np.logspace(0, int(maxn), 100, base=2.0))

These can be used for fitting the ARMAV model and retrieve the coefficients for the five most common sources of variability (quantization, angle/velocity random walk, bias instability, rate random walk, and rate ramp).

# Silence warning for inability to estimate parameter covariances, which
# is not a concern as we are not making inferences
with warnings.catch_warnings():
    warnings.simplefilter("ignore", OptimizeWarning)
    allan_coefs, adevs = imu.allan_coefs("angular_velocity", taus)

print(allan_coefs)

     angular_velocity_x  angular_velocity_y  angular_velocity_z
Q             1.008e-08           1.860e-08           5.619e-08
ARW           6.530e-04           7.559e-04           8.339e-04
BI            1.011e-04           1.400e-04           8.288e-05
RRW           1.966e-06           1.547e-10           7.758e-10
RR            4.434e-08           6.910e-08           2.854e-08

Feel free to download a copy of this demo (demo_allan.py).