Simulating bouts#

This follows the simulation of mixed Poisson distributions in Luque & Guinet (2007), and the comparison of models for characterizing such distributions.

Set up the environment.

1# Set up
2import numpy as np
3import pandas as pd
4import matplotlib.pyplot as plt
5import skdiveMove.bouts as skbouts
6
7# For figure sizes
8_FIG3X1 = (9, 12)

Generate two-process mixture#

For a mixed distribution of two random Poisson processes with a mixing parameter \(p=0.7\), and density parameters \(\lambda_f=0.05\), and \(\lambda_s=0.005\), we use the random_mixexp function to generate samples.

Define the true values described above, grouping the parameters into a Series to simplify further operations.

12p_true = 0.7
13lda0_true = 0.05
14lda1_true = 0.005
15pars_true = pd.Series({"lambda0": lda0_true,
16                       "lambda1": lda1_true,
17                       "p": p_true})

Declare the number of simulations and the number of samples to generate:

18# Number of simulations
19nsims = 500
20# Size of each sample
21nsamp = 1000

Set up variables to accumulate simulations:

22# Set up NLS simulations
23coefs_nls = []
24# Set up MLE simulations
25coefs_mle = []
26# Fixed bounds fit 1
27p_bnd = (-2, None)
28lda0_bnd = (-5, None)
29lda1_bnd = (-10, None)
30opts1 = dict(method="L-BFGS-B",
31             bounds=(p_bnd, lda0_bnd, lda1_bnd))
32# Fixed bounds fit 2
33p_bnd = (1e-1, None)
34lda0_bnd = (1e-3, None)
35lda1_bnd = (1e-6, None)
36opts2 = dict(method="L-BFGS-B",
37             bounds=(p_bnd, lda0_bnd, lda1_bnd))

Perform the simulations in a loop, fitting the nonlinear least squares (NLS) model, and the alternative maximum likelihood (MLE) model at each iteration.

38# Set up a random number generator for efficiency
39rng = np.random.default_rng()
40# Estimate parameters `nsims` times
41for i in range(nsims):
42    x = skbouts.random_mixexp(nsamp, pars_true["p"],
43                              (pars_true[["lambda0", "lambda1"]]
44                               .to_numpy()), rng=rng)
45    # NLS
46    xbouts = skbouts.BoutsNLS(x, 5)
47    init_pars = xbouts.init_pars([80], plot=False)
48    coefs, _ = xbouts.fit(init_pars)
49    p_i = skbouts.bouts.calc_p(coefs)[0][0]  # only one here
50    coefs_i = pd.concat([coefs.loc["lambda"], pd.Series({"p": p_i})])
51    coefs_nls.append(coefs_i.to_numpy())
52
53    # MLE
54    xbouts = skbouts.BoutsMLE(x, 5)
55    init_pars = xbouts.init_pars([80], plot=False)
56    fit1, fit2 = xbouts.fit(init_pars, fit1_opts=opts1,
57                            fit2_opts=opts2)
58    coefs_mle.append(np.roll(fit2.x, -1))

Non-linear least squares (NLS)#

Collect and display NLS results from the simulations:

59nls_coefs = pd.DataFrame(np.vstack(coefs_nls),
60                         columns=["lambda0", "lambda1", "p"])
61# Centrality and variance
62nls_coefs.describe()
lambda0 lambda1 p
count 500.000 5.000e+02 500.000
mean 0.047 4.004e-03 0.729
std 0.005 4.165e-04 0.020
min 0.032 3.023e-03 0.663
25% 0.044 3.715e-03 0.715
50% 0.047 3.972e-03 0.729
75% 0.050 4.264e-03 0.743
max 0.062 5.243e-03 0.785

Maximum likelihood estimation (MLE)#

Collect and display MLE results from the simulations:

63mle_coefs = pd.DataFrame(np.vstack(coefs_mle),
64                         columns=["lambda0", "lambda1", "p"])
65# Centrality and variance
66mle_coefs.describe()
lambda0 lambda1 p
count 500.000 5.000e+02 500.000
mean 0.050 5.022e-03 0.700
std 0.003 3.700e-04 0.022
min 0.043 4.047e-03 0.630
25% 0.048 4.754e-03 0.684
50% 0.050 5.005e-03 0.700
75% 0.052 5.264e-03 0.715
max 0.059 6.106e-03 0.766

Comparing NLS vs MLE#

The bias relative to the true values of the mixed distribution can be readily assessed for NLS:

67nls_coefs.mean() - pars_true

lambda0   -3.029e-03
lambda1   -9.961e-04
p          2.865e-02
dtype: float64

and for MLE:

68mle_coefs.mean() - pars_true

lambda0    2.951e-05
lambda1    2.226e-05
p         -1.965e-04
dtype: float64

To visualize the estimates obtained throughout the simulations, we can compare density plots, along with the true parameter values:

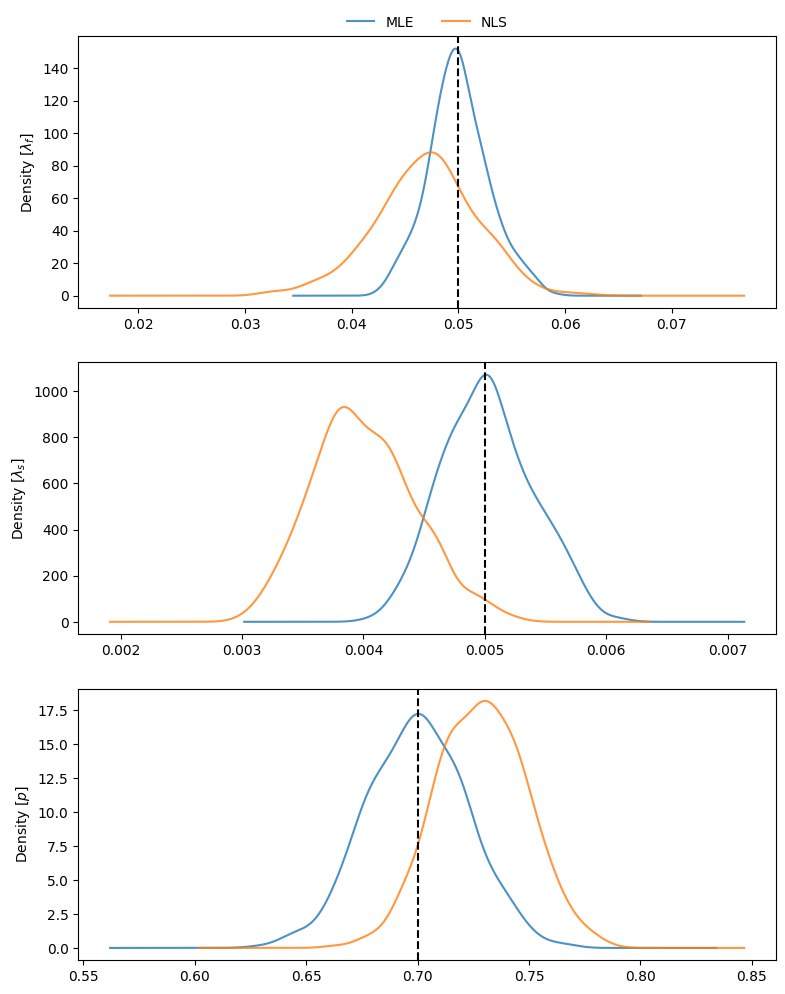
../_images/demo_simulbouts_10_0.png

Three-process mixture#

We generate a mixture of “fast”, “slow”, and “very slow” processes. The probabilities considered for modeling this mixture are \(p0\) and \(p1\), representing the proportion of “fast” to “slow” events, and the proportion of “slow” to “slow” and “very slow” events, respectively.

 93p_fast = 0.6
 94p_svs = 0.7                   # prop of slow to (slow + very slow) procs
 95p_true = [p_fast, p_svs]
 96lda_true = [0.05, 0.01, 8e-4]
 97pars_true = pd.Series({"lambda0": lda_true[0],
 98                       "lambda1": lda_true[1],
 99                       "lambda2": lda_true[2],
100                       "p0": p_true[0],
101                       "p1": p_true[1]})

Mixtures with more than two processes require careful choice of constraints to avoid numerical issues to fit the models; even the NLS model may require help.

102# Bounds for NLS fit; flattened, two per process (a, lambda).  Two-tuple
103# with lower and upper bounds for each parameter.
104nls_opts = dict(bounds=(
105    ([100, 1e-3, 100, 1e-3, 100, 1e-6]),
106    ([5e4, 1, 5e4, 1, 5e4, 1])))
107# Fixed bounds MLE fit 1
108p0_bnd = (-5, None)
109p1_bnd = (-5, None)
110lda0_bnd = (-6, None)
111lda1_bnd = (-8, None)
112lda2_bnd = (-12, None)
113opts1 = dict(method="L-BFGS-B",
114             bounds=(p0_bnd, p1_bnd, lda0_bnd, lda1_bnd, lda2_bnd))
115# Fixed bounds MLE fit 2
116p0_bnd = (1e-3, 9.9e-1)
117p1_bnd = (1e-3, 9.9e-1)
118lda0_bnd = (2e-2, 1e-1)
119lda1_bnd = (3e-3, 5e-2)
120lda2_bnd = (1e-5, 1e-3)
121opts2 = dict(method="L-BFGS-B",
122             bounds=(p0_bnd, p1_bnd, lda0_bnd, lda1_bnd, lda2_bnd))
123
124x = skbouts.random_mixexp(nsamp, [pars_true["p0"], pars_true["p1"]],
125                          [pars_true["lambda0"], pars_true["lambda1"],
126                           pars_true["lambda2"]], rng=rng)

We fit the three-process data with the two models:

127x_nls = skbouts.BoutsNLS(x, 5)
128init_pars = x_nls.init_pars([75, 220], plot=False)
129coefs, _ = x_nls.fit(init_pars, **nls_opts)
130
131x_mle = skbouts.BoutsMLE(x, 5)
132init_pars = x_mle.init_pars([75, 220], plot=False)
133fit1, fit2 = x_mle.fit(init_pars, fit1_opts=opts1,
134                       fit2_opts=opts2)

Plot both fits and BECs:

135fig, axs = plt.subplots(1, 2, figsize=(13, 5))
136x_nls.plot_fit(coefs, ax=axs[0])
137x_mle.plot_fit(fit2, ax=axs[1]);
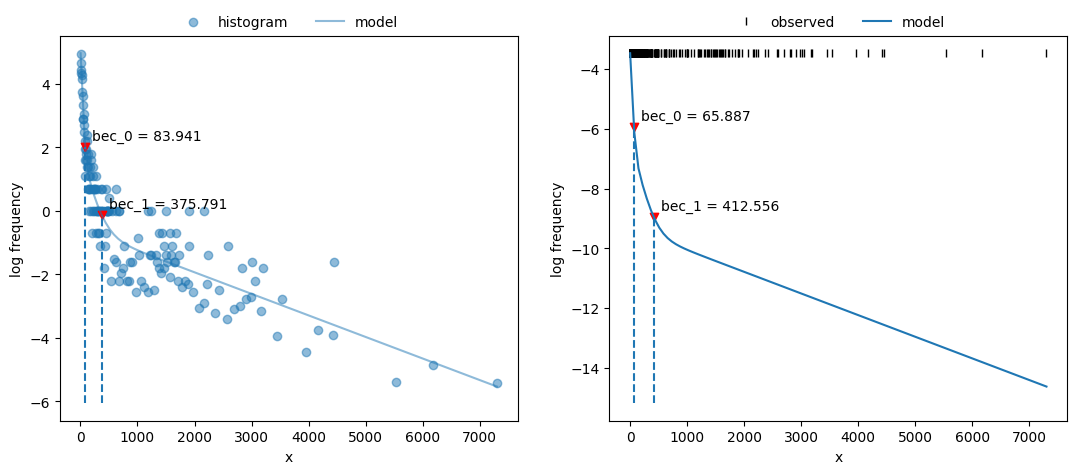
../_images/demo_simulbouts_14_0.png

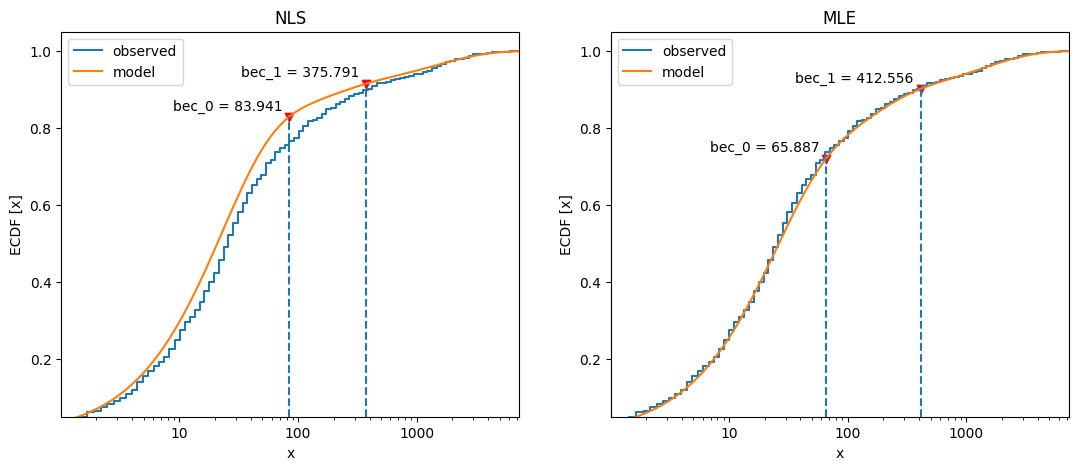
Compare cumulative frequency distributions:

138fig, axs = plt.subplots(1, 2, figsize=(13, 5))
139axs[0].set_title("NLS")
140x_nls.plot_ecdf(coefs, ax=axs[0])
141axs[1].set_title("MLE")
142x_mle.plot_ecdf(fit2, ax=axs[1]);
../_images/demo_simulbouts_15_0.png

Feel free to download a copy of this demo (demo_simulbouts.py).

On this page
Show Source