Inertial Measurement Unit time series#

Tools and classes for common IMU data processing tasks

The IMUBase represents tri-axial Inertial Measurement Unit (IMU) data to study 3D kinematics. IMU devices are often deployed together with time-depth recorders (TDR). The base class provides essential accessors and other methods to perform error analysis and compute orientation using a variety of algorithms, leveraging on the capabilities of Python package AHRS.

Base class & methods summary#

`IMUBase`(dataset[, acceleration_name, ...])	Define IMU data source
`IMUBase.read_netcdf`(imu_file[, ...])	Instantiate object by loading Dataset from NetCDF file
`IMUBase.allan_coefs`(sensor, taus)	Estimate Allan deviation coefficients for each error type
`IMUBase.compute_orientation`([method])	Compute the orientation of IMU tri-axial signals
`IMUBase.dead_reckon`([g, Wn, k])	Calculate position assuming orientation is already known

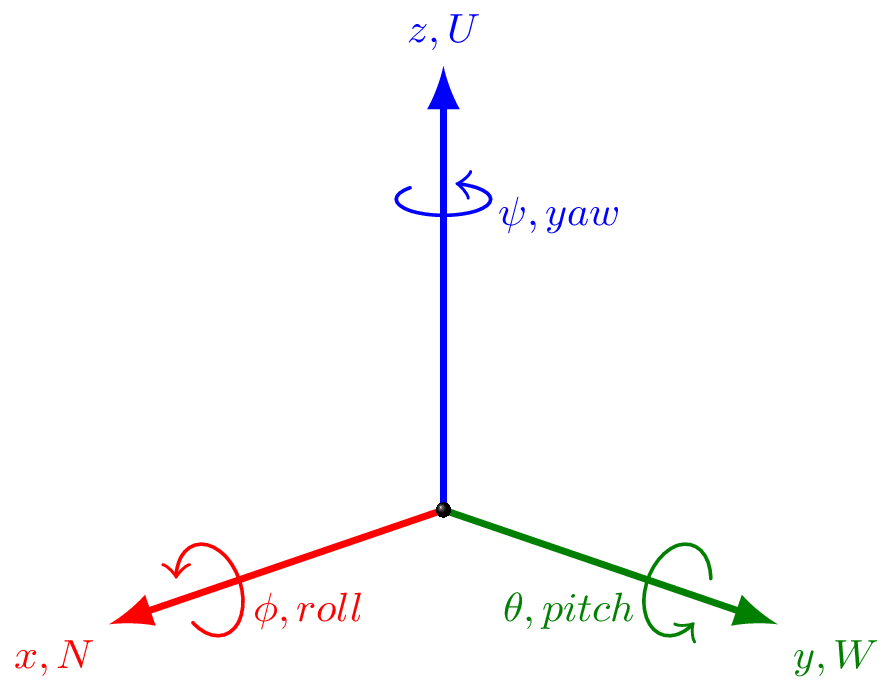
Instrument frame to body frame transformations#

One of the first tasks in analysis of IMU data from devices mounted on wild animals is estimating the orientation of the instrument on the animal. The IMU2Body class facilitates this process for devices mounted on air-breathing marine/aquatic animals that regularly come up to the surface to breathe. See Johnson (2011) for details on the approach.

Notes

A right-handed coordinate system is assumed in the input IMU data.

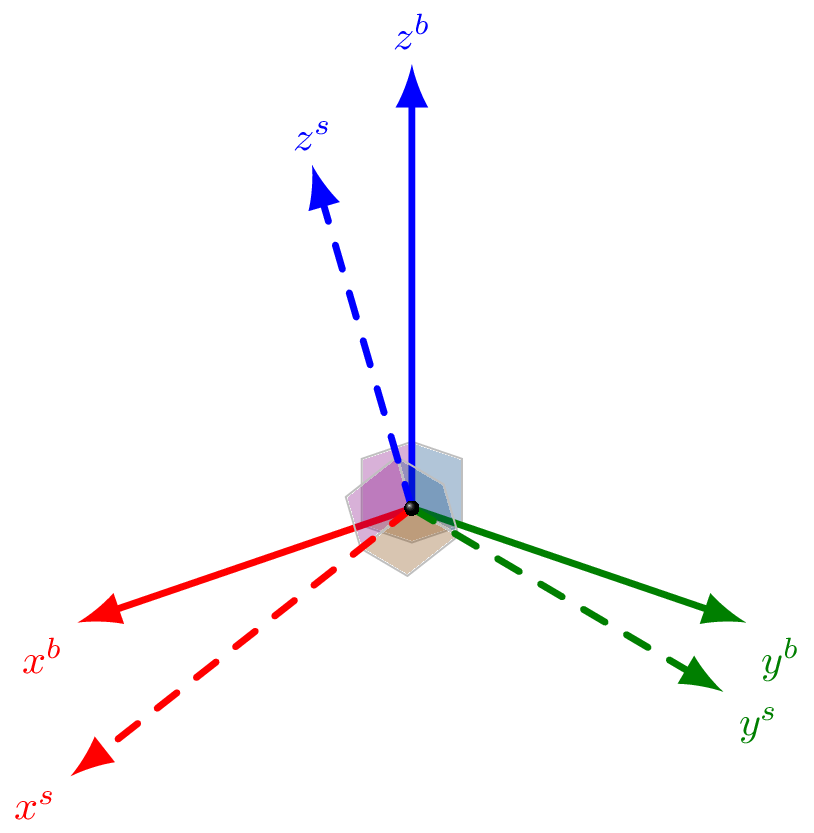
IMU2Body subclass extends IMUBase, providing an integrated approach to estimating the relative orientation of two reference frames: a) body (b) and b) sensor (s). It adds the methods summarized below.

`IMU2Body`(surface_details[, savgol_parms])	IMU coordinate frame transformation framework
`IMU2Body.from_csv_nc`(surface_details_csv, imu_nc)	Create IMU2Body from NetCDF and CSV surface details files
`IMU2Body.get_surface_vectors`(surface_idx, name)	Subset vectors of given name from IMU object for given index
`IMU2Body.get_orientation`(surface_idx[, plot])	Compute orientation for a given index in surface details table
`IMU2Body.get_orientations`()	Obtain orientation for all periods in surface details table
`IMU2Body.orient_surfacing`(surface_idx, R_b2i)	Apply orientation for a given index in surface details table
`IMU2Body.orient_surfacings`([R_all])	Apply orientation to all periods in surface details table
`IMU2Body.orient_IMU`([R_all])	Apply orientations to the IMU object
`IMU2Body.filter_surfacings`(qual_thresh)	Filter records from surface_details and orientations
`IMU2Body.scatterIMU3D`(surface_idx, vec_name)	Class plotting wrapper for module-level function
`IMU2Body.tsplotIMU_depth`(vec_name[, ...])	Class plotting wrapper for module-level function

Calibration and error analysis#

IMU measurements are generally affected by temperature, contain offsets and are affected by the error characteristics of the sensors making the measurements. These need to be taken into account and the IMUcalibrate class provides a practical framework to do so.

`IMUcalibrate`(x_calib, periods[, axis_order])	Calibration framework for IMU measurements
`IMUcalibrate.build_tmodels`(var[, T_alpha, ...])	Build temperature models for experimental tri-axial IMU sensor signals
`IMUcalibrate.plot_experiment`(period_idx, var)	Plot experimental IMU
`IMUcalibrate.plot_var_model`(var[, ...])	Plot IMU variable against temperature and fitted model
`IMUcalibrate.plot_standardized`(var[, ...])	Plot IMU measured and standardized variable along with temperature
`IMUcalibrate.get_model`(var, period[, axis])	Retrieve linear model for a given IMU sensor axis signal
`IMUcalibrate.get_offset`(var, period, ...[, axis])	Calculate signal ofset at given temperature from calibration model
`IMUcalibrate.apply_model`(var, dataset[, ...])	Apply fitted temperature compensation model to Dataset
`fit_ellipsoid`(vectors[, f])	Fit a (non) rotated ellipsoid or sphere to 3D vector data
`apply_ellipsoid`(vectors, offset, gain, rotM, ...)	Apply ellipsoid fit to vector array

class imutools.IMU2Body(surface_details, savgol_parms=None, **kwargs)[source]#

Bases: IMUBase

IMU coordinate frame transformation framework

The framework is based on the analytical approach taken in TagTools (Matlab). However, the estimation of the IMU orientation uses the covariance matrix, rather than the unscaled correlation (outer product) of acceleration as the input for Singular Value Decomposition.

In addition to attributes in IMUBase, IMU2Body adds the attributes listed below.

surface_details#

Type:: pandas.DataFrame

accel_sg#

Smoothed acceleration signals, if so requested. Otherwise, a pointer to the input acceleration signals.

Type:: pandas.DataFrame

orientations#

A summary table describing the orientation of the IMU relative to the body frame for each surface period.

Type:: pandas.DataFrame

Examples

Construct IMU2Body from NetCDF file with IMU signals, and comma-separated file with timestamps for surface periods:

>>> import importlib.resources as rsrc
>>> import skdiveMove.imutools as imutools
>>> icdf = (rsrc.files("skdiveMove") / "tests" / "data" / "gertrude" /
...         "gert_imu_frame.nc")
>>> icsv = (rsrc.files("skdiveMove") / "tests" / "data" / "gertrude" /
...         "gert_long_srfc.csv")

Apply Savitzky-Golay filter to acceleration to use as source data for Singular Value Decomposition. The required parameters for the filter are (in a tuple): 1) window length and 2) polynomial order, in that order.

>>> imu = imutools.IMU2Body.from_csv_nc(icsv, icdf,
...                                     savgol_parms=(99, 2))
>>> print(imu)  
IMU -- Class IMU2Body object
Source File           ...
IMU: <xarray.Dataset> ...
Dimensions:           ...
Coordinates:
  * timestamp         (timestamp) datetime64[ns] ...
  * accelerometer     (accelerometer) <U1 12B 'x' 'y' 'z'
  * magnetometer      (magnetometer) <U1 12B 'x' 'y' 'z'
  * gyroscope         (gyroscope) <U1 12B 'x' 'y' 'z'
Data variables:
    depth             (timestamp) float64 ...
    acceleration      (timestamp, accelerometer) float64 ...
    magnetic_density  (timestamp, magnetometer) float64 ...
    angular_velocity  (timestamp, gyroscope) float64 ...
Attributes:...
    animal_id:              Unknown
    animal_species_common:  Humpback whale
    animal_species_name:    Megaptera novaeangliae
    deployment_id:          gert01
    source_files:           gertrude_2017.csv,...
Surface segment duration summary:
count                           68
mean     0 days 00:02:01.764705882
std      0 days 00:02:15.182918382
min                0 days 00:00:11
25%         0 days 00:00:29.750000
50%                0 days 00:00:59
75%         0 days 00:02:26.250000
max                0 days 00:08:43
dtype: object

See IMU-frame to body-frame transformations demo for an extended example of typical usage of the methods in this class.

describe_surfacing_durations()[source]#

Return a summary of surfacing durations

Returns:: Summary description of durations
Return type:: pandas.Series

See also

filter_surfacings

filter_surfacings(qual_thresh)[source]#

Filter records from surface_details and orientations

Remove records from the surface_details and orientations attributes, based on quality and, optionally, duration of the surface period. Records with quality higher than the specified value, and (optionally) duration lower than the specified number of seconds, are removed.

Parameters:: qual_thresh (tuple) – Tuple with quality index and standard deviation of rolling motion during surface periods, in that order. Records with quality value higher, and standard deviation of rolling motion higher than these thresholds are removed.

See also

describe_surfacing_durations

classmethod from_csv_nc(surface_details_csv, imu_nc, endasc_col=0, beg_surface_col=5, end_surface_col=6, beg_next_desc_col=7, savgol_parms=None, load_dataset_kwargs={}, **kwargs)[source]#

Create IMU2Body from NetCDF and CSV surface details files

Utility function to facilitate reading and reshaping data files into and IMU2Body instance.

Parameters:

surface_details_csv (str) – Path to CSV file with details of long surface intervals.
imu_nc (str) – Path to NetCDF file with IMU data.
endasc_col (int) – Index of the column with the timestamps identifying the end of ascent.
beg_surface_col (int) – Index of the column with the timestamps identifying the beginning of the surface interval.
end_surface_col (int) – Index of the column with the timestamps identifying the end of the surface interval.
beg_next_desc_col (int) – Index of the column with the timestamps identifying the beginning of the next interval.
savgol_parms (tuple, optional) – A 2-element tuple with the window length and polynomial order for the Savitzky-Golay filter (savgol_filter()) to smooth acceleration.
load_dataset_kwargs (dict, optional) – Dictionary of optional keyword arguments passed to xarray.load_dataset().
**kwargs – Optional keyword arguments passed to IMUBase.__init__() method, except has_depth or imu_filename. The input Dataset is assumed to have a depth DataArray.

Return type:

IMU2Body

get_orientation(surface_idx, plot=True, **kwargs)[source]#

Compute orientation for a given index in surface details table

The orientation is computed via Singular Value Decomposition (SVD), assuming that the chosen IMU data correspond to the animal close to the surface and moving with negligible pitching and rolling motions.

The function returns the rotation from the animal body frame to the IMU frame, along with the SVD matrices. Note that a right-handed coordinate system is assumed.

Parameters:

surface_idx (datetime64) – Index in surface details table to be analyzed.
plot (bool, optional) – Whether to generate a plot of the estimate
**kwargs – Optional keyword arguments passed to scatterIMU_svd(). Only title and animate are taken.

Returns:

Rotation, (U, S, V) – Rotation object with potentially modified left singular vectors from Singular Value Decomposition (SVD), and full matrices from SVD (left singular vectors, sigma, and right singular vectors).

Return type:

tuple

Notes

The reference frame for the output Rotation object is defined by the centered acceleration vectors. All three components of this reference frame point in the positive direction of the centered data. Furthermore, this rotation is not identical to the left singular vectors because it has been flipped 180 degrees so that the rotated acceleration is negatively related to the depth gradient, as it should. Therefore, a copy of that basis was transformed by flipping the signs of these components so as to match the right-handed coordinate system assumed in the class.

get_orientations()[source]#

Obtain orientation for all periods in surface details table

A quality index (\(q\)) for each estimate is calculated as:

\[q = \frac{s_{3}}{s_{2}}\]

where the dividend and divisor are the singular values for the third and second singular vectors, respectively. A second indicator of the quality of the estimates is given as the standard deviation of the projection of the acceleration vector onto the second singular vector (i.e. pitching axis).

Returns:

DataFrame indexed the by the rows of the surface details table, and having the following columns:

R: Rotation

SVD: SVD matrices

quality: Tuple (quality index, std) for the estimate

phi: Roll angle (degrees) from body to IMU frame

theta: Pitch angle (degrees) from body to IMU frame

psi: Yaw angle (degrees) from body to IMU frame

Return type:

pandas.DataFrame

See also

get_orientation

get_surface_vectors(surface_idx, name, smoothed_accel=False)[source]#

Subset vectors of given name from IMU object for given index

Return vectors of given name from IMU object for given index in surface details table.

Parameters:

surface_idx (datetime64) – Index in surface details table to be analyzed.
name (str, {"acceleration", "magnetic_density", "depth"}) – Name of the vector array to subset.
smoothed_accel (bool, optional) – Whether to return the smoothed acceleration (if name="acceleration")

Returns:

vectors

Return type:

xarray.DataArray

orient_IMU(R_all=None)[source]#

Apply orientations to the IMU object

Use the rotations for each surface period segment to re-orient the IMU object to the animal frame. Alternatively, apply the supplied rotation to the entire IMU object.

An overview of the re-orientation process is illustrated below.

Each surface segment \(s_i\), delineated by beginning and ending times \(t_{0}^{s_i}\) and \(t_{1}^{s_i}\) (\(i=1\) to \(i=n\)), respectively, allows for an estimate of the IMU device orientation on the animal. The corresponding rotation \(R_{s_{i}}\) for transforming data from the IMU frame to the animal frame is applied to the data segments in the second line above, from the beginning of the deployment at \(t_0\) to the end at \(t_k\).

Parameters:: R_all (Rotation, optional) – A Rotation object representing the rotation from the centered body frame to the IMU frame to be applied to the entire IMU object.
Returns:: Dataset with the re-oriented IMU object. If R_all was not provided, the Dataset contains an additional coordinate representing the surfacing period for each segment.
Return type:: xarray.Dataset

See also

orient_surfacing, orient_surfacings

orient_surfacing(surface_idx, R_b2i)[source]#

Apply orientation for a given index in surface details table

Re-orient acceleration and magnetic density of IMU object relative to body frame, and return re-oriented IMU object. Note that the provided R_b2i must describe the rotation from the body frame to the IMU frame. The opposite rotation is applied to the acceleration and magnetic field vectors of the selected surface segment to orient the data in the body frame.

Parameters:

surface_idx (datetime64) – Index in surface details table to be analyzed.
R_b2i (Rotation) – Rotation object representing the rotation from the body frame to the IMU frame.

Returns:

The re-oriented IMU object.

Return type:

xarray.Dataset

See also

orient_surfacings, orient_IMU

orient_surfacings(R_all=None)[source]#

Apply orientation to all periods in surface details table

If the orientations attribute was filled, use it to build multi-index dataframe, othewise, fill it.

This method orients each segment independently, as opposed to a “smooth” transition between segments. Use IMU2Body.orient_IMU() once satisfied with the results from individual segments to achieve a smooth adjustment of orientation across segments.

Parameters:: R_all (Rotation, optional) – A Rotation object representing the rotation from the centered body frame to the IMU frame to be applied to all surface periods. Default is to use the period-specific rotation.
Returns:: Dataset with the re-oriented surface IMU objects. If R_all was not provided, the Dataset contains an additional coordinate representing the surfacing period for each segment.
Return type:: xarray.Dataset

See also

orient_surfacing, orient_IMU

scatterIMU3D(surface_idx, vec_name, smoothed_accel=False, **kwargs)[source]#

Class plotting wrapper for module-level function

Parameters:

surface_idx (datetime64) – Index in surface details table to be analyzed.
vec_name (str, {"acceleration", "magnetic_density"}) – Name of the vector array to subset.
smoothed_accel (bool, optional) – Whether to plot the smoothed acceleration (if vec_name=”acceleration”)
**kwargs – Optional keyword arguments passed to scatterIMU3D().

Returns:

Axes

Return type:

matplotlib.axes.Axes

See also

tsplotIMU_depth

tsplotIMU_depth(vec_name, surface_idx=None, smoothed_accel=False, **kwargs)[source]#

Class plotting wrapper for module-level function

Plot selected vector along with depth for the entire time series, and the edges of all surface segments overlaid on the depth panel. Alternatively, a specific surface segment can be plotted individually.

Parameters:

vec_name (str, {"acceleration", "magnetic_density"}) – Name of the vector array to subset.
surface_idx (datetime64, optional) – Index in surface details table to be analyzed.
smoothed_accel (bool, optional) – Whether to plot the smoothed acceleration (if vec_name=”acceleration”)
**kwargs – Optional keyword arguments passed to subplots() (e.g. figsize).

Returns:

Array with matplotlib.axes.Axes instances.

Return type:

array_like

See also

scatterIMU3D

class imutools.IMUBase(dataset, acceleration_name='acceleration', angular_velocity_name='angular_velocity', magnetic_density_name='magnetic_density', time_name='timestamp', has_depth=False, depth_name='depth', imu_filename=None)[source]#

Bases: object

Define IMU data source

Use xarray.Dataset to ensure pseudo-standard metadata.

imu_file#

String indicating the file where the data comes from.

Type:: str

imu#

Dataset with input data.

Type:: xarray.Dataset

imu_var_names#

Names of the data variables with accelerometer, angular velocity, and magnetic density measurements.

Type:: list

has_depth#

Whether input data include depth measurements.

Type:: bool

depth_name#

Name of the data variable with depth measurements.

Type:: str

time_name#

Name of the time dimension in the dataset.

Type:: str

quats#

Array of quaternions representing the orientation relative to the frame of the IMU object data. Note that the scalar component is last, following scipy’s convention.

Type:: numpy.ndarray

Examples

This example illustrates some of the issues encountered while reading data files in a real-world scenario. scikit-diveMove includes a NetCDF file with IMU signals collected using a Samsung Galaxy S5 mobile phone. Set up instance from NetCDF example data:

>>> import importlib.resources as rsrc
>>> import xarray as xr
>>> import skdiveMove.imutools as imutools
>>> icdf = (rsrc.files("skdiveMove") / "tests" / "data" /
...         "samsung_galaxy_s5.nc")

The angular velocity and magnetic density arrays have two sets of measurements: output and measured, which, along with the sensor axis designation, constitutes a multi-index. These multi-indices can be rebuilt prior to instantiating IMUBase, as they provide significant advantages for indexing later:

>>> s5ds = (xr.load_dataset(icdf)
...         .set_index(gyroscope=["gyroscope_type", "gyroscope_axis"],
...                    magnetometer=["magnetometer_type",
...                                  "magnetometer_axis"]))
>>> imu = imutools.IMUBase(s5ds.sel(gyroscope="output",
...                                 magnetometer="output"),
...                        imu_filename=icdf)

See Allan deviation analysis demo for an extended example of typical usage of the methods in this class.

allan_coefs(sensor, taus)[source]#

Estimate Allan deviation coefficients for each error type

This procedure implements the autonomous regression method for Allan variance described in [1].

Given averaging intervals taus and corresponding Allan deviation adevs, compute the Allan deviation coefficient for each error type:

Quantization

(Angle, Velocity) Random Walk

Bias Instability

Rate Random Walk

Rate Ramp

Parameters:

sensor (str) – Attribute name of the sensor of interest
taus ({float, str}) – Tau value, in seconds, for which to compute statistic. Can be one of “octave” or “decade” for automatic generation of the value.

Returns:

coefs_all (pandas.DataFrame) – Allan deviation coefficient and corresponding averaging time for each sensor axis and error type.
adevs (pandas.DataFrame) – MultiIndex DataFrame with Allan deviation, corresponding averaging time, and fitted ARMAV model estimates of the coefficients for each sensor axis and error type.

Notes

Currently uses a modified Allan deviation formula.

compute_orientation(method='Madgwick', **kwargs)[source]#

Compute the orientation of IMU tri-axial signals

The method must be one of the following estimators implemented in Python module ahrs.filters:

AngularRate: Attitude from angular rate

AQUA: Algebraic quaternion algorithm

Complementary: Complementary filter

Davenport: Davenport’s q-method

EKF: Extended Kalman filter

FAAM: Fast accelerometer-magnetometer combination

FLAE: Fast linear attitude estimator

Fourati: Fourati’s nonlinear attitude estimation

FQA: Factored quaternion algorithm

Madgwick: Madgwick orientation filter

Mahony: Mahony orientation filter

OLEQ: Optimal linear estimator quaternion

QUEST

ROLEQ: Recursive optimal linear estimator of quaternion

SAAM: Super-fast attitude from accelerometer and magnetometer

Tilt: Attitude from gravity

The estimated quaternions are stored in the quats attribute.

Parameters:

method (str, optional) – Name of the filtering method to use.
**kwargs – Optional keyword arguments passed to filtering method.

dead_reckon(g=9.80665, Wn=1.0, k=1.0)[source]#

Calculate position assuming orientation is already known

Integrate dynamic acceleration in the body frame to calculate velocity and position. If the IMU instance has a depth signal, it is used in the integration instead of acceleration in the vertical dimension.

Parameters:

g (float, optional) – Assume gravity (\(m / s^2\)) is equal to this value. Default to standard gravity.
Wn (float, optional) – Cutoff frequency for second-order Butterworth lowpass filter.
k (float, optional) – Scalar to apply to scale lowpass-filtered dynamic acceleration. This scaling has the effect of making position estimates realistic for dead-reckoning tracking purposes.

Returns:

vel, pos – Velocity and position 2D arrays.

Return type:

numpy.ndarray

classmethod read_netcdf(imu_file, acceleration_name='acceleration', angular_velocity_name='angular_velocity', magnetic_density_name='magnetic_density', time_name='timestamp', has_depth=False, depth_name='depth', **kwargs)[source]#

Instantiate object by loading Dataset from NetCDF file

Provided all DataArrays in the NetCDF file have the same dimensions (N, 3), this is an efficient way to instantiate.

Parameters:

imu_file (str) – As first argument for xarray.load_dataset().
acceleration_name (str, optional) – Name of the acceleration DataArray in the Dataset.
angular_velocity_name (str, optional) – Name of the angular velocity DataArray in the Dataset.
magnetic_density_name (str, optional) – Name of the magnetic density DataArray in the Dataset.
has_depth (bool, optional) – Whether input data include depth measurements.
depth_name (str, optional) – Name of the depth DataArray in the Dataset.
**kwargs – Optional keyword arguments passed to xarray.load_dataset().

Returns:

obj – Class matches the caller.

Return type:

IMUBase

property acceleration#

Return acceleration array

Return type:: xarray.DataArray

property angular_velocity#

Return angular velocity array

Return type:: xarray.DataArray

property depth#

Return depth array

Return type:: xarray.DataArray

property magnetic_density#

Return magnetic_density array

Return type:: xarray.DataArray

property sampling_interval#

Return sampling interval

Assuming all DataArray`s have the same interval, the sampling interval is retrieved from the acceleration `DataArray.

Return type:: xarray.DataArray

Warning

The sampling rate is retrieved from the attribute named sampling_rate in the NetCDF file, which is assumed to be in Hz units.

class imutools.IMUcalibrate(x_calib, periods, axis_order=['x', 'y', 'z'], **kwargs)[source]#

Bases: IMUBase

Calibration framework for IMU measurements

Measurements from most IMU sensors are influenced by temperature, among other artifacts. The IMUcalibrate class implements the following procedure to remove the effects of temperature from IMU signals:

For each axis, fit a piecewise or simple linear regression of measured (lowpass-filtered) data against temperature.
Compute predicted signal from the model.
Select a reference temperature \(T_{\alpha}\) to standardize all measurements at.
The standardized measurement (\(x_\sigma\)) at \(T_{\alpha}\) is calculated as:

(1)#\[x_\sigma = x - (\hat{x} - \hat{x}_{\alpha})\]

where \(\hat{x}\) is the value predicted from the model at the measured temperature, and \(\hat{x}_{\alpha}\) is the predicted value at \(T_{\alpha}\).

The models fit to signals from a motionless (i.e. experimental) IMU device in the first step can subsequently be used to remove or minimize temperature effects from an IMU device measuring motions of interest, provided the temperature is within the range observed in experiments.

In addition to attributes in IMUBase, IMUcalibrate adds the attributes listed below.

periods#

List of slices with the beginning and ending timestamps defining periods in x_calib where valid calibration data are available. Periods are assumed to be ordered chronologically.

Type:: list

models_l#

List of dictionaries as long as there are periods, with each element corresponding to a sensor, in turn containing another dictionary with each element corresponding to each sensor axis.

Type:: list

axis_order#

List of characters specifying which axis x, y, or z was pointing in the same direction as gravity in each period in periods.

Type:: list

Examples

Construct IMUcalibrate from NetCDF file with samples of IMU signals and a list with begining and ending timestamps for experimental periods:

>>> import importlib.resources as rsrc
>>> import skdiveMove.imutools as imutools
>>> icdf = (rsrc.files("skdiveMove") / "tests" / "data" /
...         "cats_temperature_calib.nc")
>>> pers = [slice("2021-09-20T09:00:00", "2021-09-21T10:33:00"),
...         slice("2021-09-21T10:40:00", "2021-09-22T11:55:00"),
...         slice("2021-09-22T12:14:00", "2021-09-23T11:19:00")]
>>> imucal = (imutools.IMUcalibrate
...           .read_netcdf(icdf, periods=pers,
...                        axis_order=list("zxy"),
...                        time_name="timestamp_utc"))
>>> print(imucal)  
IMU -- Class IMUcalibrate object
Source File          None
IMU: <xarray.Dataset> ...
Dimensions:           (timestamp_utc: 268081, axis: 3)
Coordinates:
  * axis              (axis) <U1 12B 'x' 'y' 'z'
  * timestamp_utc     (timestamp_utc) datetime64[ns] ...
Data variables:
    acceleration      (timestamp_utc, axis) float64 ...
    angular_velocity  (timestamp_utc, axis) float64 ...
    magnetic_density  (timestamp_utc, axis) float64 ...
    depth             (timestamp_utc) float64 ...
    temperature       (timestamp_utc) float64 ...
Attributes:...
    history:  Resampled from 20 Hz to 1 Hz
Periods:
0:['2021-09-20T09:00:00', '2021-09-21T10:33:00']
1:['2021-09-21T10:40:00', '2021-09-22T11:55:00']
2:['2021-09-22T12:14:00', '2021-09-23T11:19:00']

Plot signals from a given period:

>>> fig, axs, axs_temp = imucal.plot_experiment(0, var="acceleration")

Build temperature models for a given variable and chosen \(T_{\alpha}\), without low-pass filtering the input signals:

>>> fs = 1.0
>>> acc_cal = imucal.build_tmodels("acceleration", T_alpha=8,
...                                use_axis_order=True,
...                                 win_len=int(2 * 60 * fs) - 1)

Plot model of IMU variable against temperature:

>>> fig, axs = imucal.plot_var_model("acceleration",
...                                  use_axis_order=True)

Notes

This class redefines IMUBase.read_netcdf().

apply_model(var, dataset, T_alpha=None, ref_vals=None, use_axis_order=True, model_idx=None)[source]#

Apply fitted temperature compensation model to Dataset

The selected models for tri-axial sensor data are applied to input Dataset, standardizing signals at \(T_{\alpha}\), optionally subtracting the offset at \(T_{\alpha}\).

Parameters:

var (str) – Name of the variable with tri-axial data.
dataset (xarray.Dataset) – Dataset with temperature and tri-axial data from motionless IMU.
T_alpha (float, optional) – Reference temperature at which all measurements will be adjusted to. Default is the mean temperature in the input dataset.
ref_vals (list, optional) – Sequence of three floats with target values to compare against the signal from each sensor axis. If provided, the offset of each signal at \(T_{\alpha}\) is computed and subtracted from the temperature-standardized signal. The order should be the same as in the axis_order attribute if use_axis_order is True, or x, y, z otherwise.
use_axis_order (bool, optional) – Whether to use axis order from the instance. If True, retrieve model to apply using instance’s axis_order attribute. Otherwise, use the models defined by model_idx argument. Ignored if var is monoaxial.
model_idx (list or int, optional) – Sequence of three integers identifying the period (zero-based) from which to retrieve the models for x, y, and z sensor axes, in that order. If var is monoaxial, an integer specifying the period for the model to use. Ignored if use_axis_order is True.

Return type:

xarray.Dataset

build_tmodels(var, T_alpha=None, T_brk=None, use_axis_order=False, filter_sig=True, **kwargs)[source]#

Build temperature models for experimental tri-axial IMU sensor signals

Perform thermal compensation on motionless tri-axial IMU sensor data. A simple approach is used for the compensation:

For each axis, build a piecewise or simple linear regression of measured data against temperature. If a breakpoint is known, as per manufacturer specifications or experimentation, use piecewise regression.

Compute predicted signal from the model.

Select a reference temperature \(T_{\alpha}\) to standardize all measurements at.

The standardized measurement at \(T_{\alpha}\) is calculated as \(x - (\hat{x} - x_{T_{\alpha}})\), where \(\hat{x}\) is the value predicted from the model at the measured temperature, and \(x_{T_{\alpha}}\) is the predicted value at \(T_{\alpha}\).

Parameters:

var (str) – Name of the variable in x with tri-axial data.
T_alpha (float, optional) – Reference temperature at which all measurements will be adjusted to. Defaults to the mean temperature for each period, rounded to the nearest integer.
T_brk (float, optional) – Temperature change point separating data to be fit differently. A piecewise regression model is fit. Default is a simple linear model is fit.
use_axis_order (bool, optional) – Whether to use axis order from the instance. If True, only one sensor axis per period is considered to have valid calibration data for the correction. Otherwise, all three axes for each period are used in the correction.
filter_sig (bool, optional) – Whether to filter in the measured signal for thermal correction. Default is to apply a Savitzky-Golay filter to the signal for characterizing the temperature relationship, and to calculate the standardized signal.
**kwargs – Optional keyword arguments passed to savgol_filter() (e.g. win_len and polyorder).

Returns:

List of tuples as long as there are periods, with tuple elements:

Dictionary with regression model objects for each sensor axis.

DataFrame with hierarchical column index with sensor axis label at the first level. The following columns are in the second level:

temperature

var_name

var_name_pred

var_name_temp_refC

var_name_adj

Return type:

list

Notes

A new DataArray with signal standardized at \(T_{\alpha}\) is added to the instance Dataset. These signals correspond to the lowpass-filtered form of the input used to build the models.

See also

apply_model

get_model(var, period, axis=None)[source]#

Retrieve linear model for a given IMU sensor axis signal

Parameters:

var (str) – Name of the variable to calculate offset for.
period (int) – Period containing calibration model to use.
axis (str, optional) – Name of the sensor axis the signal comes from, if var is tri-axial; ignored otherwise.

Return type:

RegressionResultsWrapper

get_offset(var, period, T_alpha, ref_val, axis=None)[source]#

Calculate signal ofset at given temperature from calibration model

Parameters:

var (str) – Name of the variable to calculate offset for.
period (int) – Period (zero-based) containing calibration model to use.
T_alpha (float) – Temperature at which to compute offset.
ref_val (float) – Reference value for the chosen variable (e.g. gravity, for acceleration).
axis (str, optional) – Name of the sensor axis the signal comes from, if var is tri-axial; ignored otherwise.

Return type:

float

Notes

For obtaining offset and gain of magnetometer signals, the ellipsoid method from the the ellipsoid module yields far more accurate results, as it allows for the simultaneous three-dimensional estimation of the offset.

plot_experiment(period_idx, var, units_label=None, **kwargs)[source]#

Plot experimental IMU

Parameters:

period_idx (int) – Index of period to plot (zero-based).
var (str) – Name of the variable in with tri-axial data.
units_label (str, optional) – Label for the units of the chosen variable. Defaults to the “units_label” attribute available in the DataArray.
**kwargs – Optional keyword arguments passed to subplots() (e.g. figsize).

Returns:

fig (matplotlib.Figure)
axs (array_like) – Array of Axes instances in fig with IMU signal plots.
axs_temp (array_like) – Array of Axes instances in fig with temperature plots.

See also

plot_var_model, plot_standardized

plot_standardized(var, use_axis_order=True, units_label=None, ref_val=None, axs=None, **kwargs)[source]#

Plot IMU measured and standardized variable along with temperature

A multi-panel time series plot of the selected variable, measured and standardized, for all periods.

Parameters:

var (str) – IMU variable to plot.
use_axis_order (bool, optional) – Whether to use axis order from the instance. If True, only one sensor axis per period is considered to have valid calibration data for the correction. Otherwise, all three axes for each period are used in the correction.
units_label (str, optional) – Label for the units of the chosen variable. Defaults to the “units_label” attribute available in the DataArray.
ref_val (float) – Reference value for the chosen variable (e.g. gravity, for acceleration). If provided, a horizontal line is included in the plot for reference.
axs (array_like, optional) – Array of Axes instances to plot in.
**kwargs – Optional keyword arguments passed to subplots() (e.g. figsize).

Returns:

fig (matplotlib.Figure)
axs (array_like) – Array of Axes instances in fig with IMU signal plots.
axs_temp (array_like) – Array of Axes instances in fig with temperature plots.

See also

plot_experiment, plot_var_model

plot_var_model(var, use_axis_order=True, units_label=None, axs=None, **kwargs)[source]#

Plot IMU variable against temperature and fitted model

A multi-panel plot of the selected variable against temperature from all periods.

Parameters:

var (str) – IMU variable to plot.
use_axis_order (bool) – Whether to use axis order from the instance. If True, only one sensor axis per period is considered to have valid calibration data for the correction. Otherwise, all three axes for each period are used in the correction. Ignored for uniaxial variables.
units_label (str) – Label for the units of the chosen variable. Defaults to the “units_label” attribute available in the DataArray.
axs (array_like, optional) – Array of Axes instances to plot in.
**kwargs – Optional keyword arguments passed to subplots() (e.g. figsize).

Returns:

fig (matplotlib.Figure)
axs (array_like) – Array of Axes instances in fig with IMU signal plots.

See also

plot_experiment, plot_standardized

classmethod read_netcdf(imu_nc, load_dataset_kwargs={}, **kwargs)[source]#

Create IMUcalibrate from NetCDF file and list of slices

This method redefines IMUBase.read_netcdf().

Parameters:

imu_nc (str) – Path to NetCDF file.
load_dataset_kwargs (dict, optional) – Dictionary of optional keyword arguments passed to xarray.load_dataset().
**kwargs – Optional keyword arguments passed to IMUcalibrate.__init__() method, except has_depth or imu_filename. The input Dataset is assumed to have a depth DataArray.

Return type:

out

savgol_filter(var, period_idx, win_len, polyorder=1)[source]#

Apply Savitzky-Golay filter on tri-axial IMU signals

Parameters:

var (str) – Name of the variable in x with tri-axial signals.
period_idx (int) – Index of period to plot (zero-based).
win_len (int) – Window length for the low pass filter.
polyorder (int, optional) – Polynomial order to use.

Returns:

Array with filtered signals, with the same coordinates, dimensions, and updated attributes.

Return type:

xarray.DataArray

subset_imu(period_idx)[source]#

Subset IMU dataset given a period index

The dataset is subset using the slice corresponding to the period index.

Parameters:: period_idx (int) – Index of the experiment period to subset.
Return type:: xarray.Dataset

imutools.apply_ellipsoid(vectors, offset, gain, rotM, ref_r)[source]#: Apply ellipsoid fit to vector array

imutools.fit_ellipsoid(vectors, f='rxyz')[source]#

Fit a (non) rotated ellipsoid or sphere to 3D vector data

Parameters:

vectors ((N,3) array) – Array of measured x, y, z vector components.
f (str) – String indicating the model to fit (one of ‘rxyz’, ‘xyz’, ‘xy’, ‘xz’, ‘yz’, or ‘sxyz’): rxyz : rotated ellipsoid (any axes) xyz : non-rotated ellipsoid xy : radius x=y xz : radius x=z yz : radius y=z sxyz : radius x=y=z sphere

Returns:

otuple – Tuple with offset, gain, and rotation matrix, in that order.

Return type:

tuple

imutools.scatterIMU3D(vectors, col_vector, normalize=True, title=None, animate=True, animate_file=None, cbar_label=None, **kwargs)[source]#

3D plotting of vectors along with depth

Scatter plot of vectors, colored by depth.

Parameters:

vectors (array_like, shape (N, 3) or (3,)) – Array with vectors to plot.
col_vector (array_like, shape (N,)) – The array to be used for coloring symbols.
normalize (bool, optional) – Whether to normalize vectors.
title (str, optional) – Title for the plot.
animate (bool, optional) – Whether to animate the plot.
animate_file (str) – Output file for the animation.
cbar_label (str, optional) – Title for the color bar.
**kwargs – Optional keyword arguments passed to figure() (e.g. figsize).

Return type:

matplotlib.axes.Axes

imutools.scatterIMU_svd(vectors, svd, R_ctr2i, normalize=False, center=False, title=None, animate=False, animate_file=None, **kwargs)[source]#

3D plotting of vectors and singular vector matrices

Plots a surface of the 2 top-most singular vectors computed from SVD overlaid on the scatter of vectors.

Parameters:

vectors (array_like, shape (N, 3) or (3,)) – Array with vectors to plot.
svd (tuple) – The 3 arrays from Singular Value Decomposition (left singular vectors, sigma, right singular vectors).
R_ctr2i (Rotation) – Rotation object describing the rotation from the centered body frame to the IMU frame.
normalize (bool, optional) – Whether to normalize vectors. Default assumes input is normalized.
center (bool, optional) – Whether to center vectors (i.e. subtract the mean). Default assumes input is centered.
title (str, optional) – Title for the plot.
animate (bool, optional) – Whether to animate the plot.
animate_file (str, optional) – Output file for the animation.
**kwargs – Optional keyword arguments passed to figure() (e.g. figsize).

Return type:

matplotlib.axes.Axes

imutools.tsplotIMU_depth(vectors, depth, time_name='timestamp', **kwargs)[source]#

Plot depth and each column of (N,3) array

Parameters:

vectors (xarray.DataArray) – Array with columns to plot in subplot.
depth (xarray.DataArray) – Array with depth measurements.
**kwargs (optional keyword arguments) – Arguments passed to subplots() (e.g. figsize).

Returns:

Array with matplotlib.axes.Axes instances.

Return type:

array_like